Ma thèse a pu montrer que les bases d'images classiquement utilisées pour les tests de qualité image ne sont pas adaptées à l'étude de l'aliasing. Nous proposons donc la base suivante composée de 5 modèles synthétiques d'images, 7 images bien échantillonnées et 7 images mal échantillonnées. Ces images regroupent les cas d'aliasing les plus caractéristiques et les cas de structures réelles ressemblant le plus à de l'aliasing.

La fabrication des images réelles de cette base de test est la suivante. Les photos ont été prises avec un appareil photo numérique Sony NEX 5, elles ont subi les opérations suivantes afin d'éliminer l'aliasing et limiter le ringing :

• décomposition p+s selon l'algorithme de Lionel Moisan
• réduction de rapport 4 par coupure spectrale de l'image périodique p.
• sous-échantillonnage de rapport 4 de l'image s.
• l'image utilisée est la somme des deux images précédentes.

Ci-dessous la description de cette base qui est téléchargeable ici.

Des modèles synthétiques

Les premières images de cette base sont des modèles synthétiques qui visent à tester des conditions d'aliasing ou non aliasing bien particulieres. Nous rajoutons à chacun de ces modèles un bruit gaussien additif afin que le fond de l'image ne soit pas auto-similaire.

Phases aléatoires

Ce modèle a déjà été présenté à plusieurs reprises dans cette thèse. Il consiste à conserver le module de la transformée de Fourier d'une image et de randomiser les phases de ces coefficients. Dans ce cas, l'image utilisée pour créer cette texture à phase aléatoire sera une image mal échantillonnée. Cette image ne correspond pas à un processus d'acquisition, il n'est donc pas aisé d'affirmer si elle a de l'aliasing ou non. Par construction, rien ne permet d'affirmer que cette image est aliasée car les zones fréquentielles en relation d'aliasing ne sont pas particulièrement corrélées spatialement.

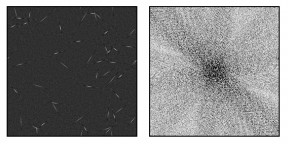
Dans les tests qui suivent et l'image fournie dans le benchmark, c'est l'image ``pdb'' de ma thèse qui a servi de source à l'algorithme et le résultat de la randomisation des phases est présenté ci-dessous :

L'image de gauche a été générée à partir de l'image ``pbd'' sous-échantillonnée de 2 et l'image de droite est le module de sa transformée de Fourier. Les modules des coefficients de la transformée de Fourier ont été conservés et les phases remplacés par des phases aléatoires. Ainsi, le module de la transformée de Fourier de cette images parait aliasé alors que l'on ne peut pas pas considérer que l'image l'est.

Bandes spectrales

On a vu que la plupart des structures directionnelles ont une grande partie de l'énergie de leur spectre inclu dans une bande contenant l'origine. Selon la structure, cette bande peut être plus ou moins étroite. Dans ce modèle, nous proposons de construire des images bien échantillonnées de structures directionnelles 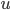$u$ définies par la transformée de Fourier suivante,

$$\hat{u}(\mu)=\mathbf{1}_{E}(\mu).e^{i<d|\mu>}$$

où

$$E=\left\{\mu\in\Omega,|<\mu|e_{\alpha}^{\perp}>|\leq r\right\}$$

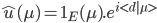
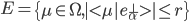
où l'on note,

$$e_{\alpha}^{\perp}=\left(-\sin(\alpha),\cos(\alpha)\right).$$

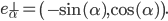
Le spectre de ces images est exclusivement contenu dans une bande contenant l'origine. Ce type d'image dépend des paramètres 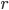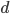$r$, $d$ et $\alpha$. Nous proposons de les tirer aléatoirement. Un exemple de ce type d'image est présenté sur la figure ci-dessous :

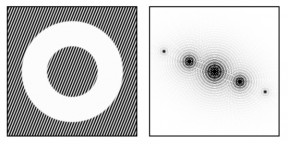
L'image de gauche est construite selon le modèle des ``bandes spectrales'', à droite est représenté le module de sa transformée de Fourier. Selon la largeur des bandes dans le spectre, des algorithmes analysant des repliements géométriques du spectre peuvent faire des erreurs.

L'image présente dans la base contient 50 de ces tirages. Nous ajoutons ensuite un bruit blanc gaussien pour éviter au fond d'être auto-similaire. L'exemple fourni dans le benchmark est présenté sur la figure ci-dessous :

L'image de gauche est construite selon le modèle des ``bandes spectrales'', on a représenté à droite le module de sa transformée de Fourier. Cet image correspond au tirage de 50 structures correspondant au modèle ``bandes spectrales''

la difficulté de la bonne analyse de ce type d'image dépend de la largeur de la bande spectrale. En effet, des raisonnements géométriques sur le spectre peuvent faire des erreurs pour des bandes spectrales très larges.

Les images de ce modèle sont construites dans le domaine de Fourier pour assurer l'absence de effet de repliement de spectre.

Angles droits

L'aliasing s'exprime le plus généralement sous la forme d'une superposition locale de deux directions. Parmi les angles possibles des deux orientations, les angles droits sont surreprésentés dans les images réelles. Nous proposons donc un modèle d'angles droits bien échantillonnés pour tester les algorithmes de détection d'aliasing sur ce type de structures.

Nous avons vu dans le paragraphe précédent comment construire une structure mono-directionnelle non aliasée, les images $u$ d'angles droit seront construits selon le même principe,

$$\hat{u}(\mu)=\textbf{1}_{E}(\mu).e^{i<d|\mu>}$$

où

$$E=\left\{\\mu\in\\Omega,|<\mu|e_{\alpha}>|\leq r\text{ ou }|<\mu|e_{\alpha}^{\perp}>|\leq r\right\}$$

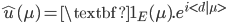
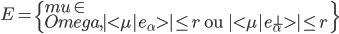
où l'on note,

$$e_{\alpha}=\left(\cos(\alpha),\sin(\alpha)\right)$$

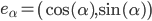
Encore une fois, 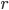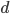$r$, $d$ et $\alpha$ seront tirés aléatoirement. Un exemple d'une structure de ce type est présenté sur la figure ci-dessous :

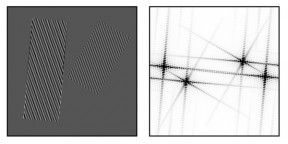
L'image de gauche est construite selon le modèle des ``angles droits''. A droite on a représenté sa transformée de Fourier. Les images réelles, en particulier urbaines, présentent un grand nombre d'angles droits. Un bon algorithme de détection ne doit pas détecter d'aliasing sur cette image.

L'image de la base comporte 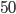$50$ de ces tirages, elle est présentée sur la figure ci-dessous Cette image n'est pas aliasées.

Angles droits.}{L'image de gauche est construite selon le modèle des ``angles droits''. A droite on a représenté sa transformée de Fourier. Ceci correspond au tirage de $50$ structures de type ``angle droit''.

cercle sur onde

Les images réelles comportent aussi bien sûr régulièrement des angles non droits. Afin de tester ces angles, nous proposons la construction suivante.

L'image 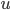$u$ est constituée d'un fond d'une structure en harmoniques ponctuelles et d'un anneau. La transformée de Fourier d'un disque est connue grâce à la fonction de Bessel d'ordre 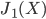$1$, $J_{1}(X)$. Pour la fonction disque de rayon $1$.

$$\mathcal{F}\left(\text{circ}(X)\right)=\frac{J_{1}(\|\mu\|)}{\|\mu\|}$$

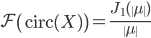
où circ est la fonction indicatrice d'un disque de rayon $1$.

Un anneau bien échantillonné 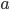$a$ est défini par sa transformée de Fourier

$$\hat{a}_{r_{1},r_{2}}(\mu)=\left(\frac{J_{1}\left(\frac{\|\mu\|}{r_{2}}\right)}{\|\mu\|}-\frac{J_{1}\left(\frac{\|\mu\|}{r_{1}}\right)}{\|\mu\|}\right).\mathbb{1}_{\Omega}(\mu)$$

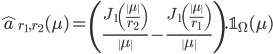
où 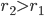$r_{2}>r_{1}$. le fond à harmoniques 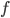$f$ est quant à lui défini par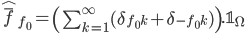

$$\hat{\bar{f}}_{f_{0}}=\left(\sum_{k=1}^{\infty}(\delta_{f_{0}k}+\delta_{-f_{0}k})\right).\mathbb{1}_{\Omega}$$

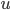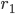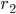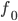Les images $u$ de ce modèle dépendent des trois paramètres $r_{1}$, $r_{2}$ et $f_{0}$, elles sont définies par leur transformée de Fourier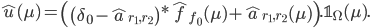

$$\hat{u}(\mu)=\left(\left(\delta_{0}-\hat{a}_{r_{1},r_{2}}\right)*\hat{f}_{f_{0}}(\mu)+\hat{a}_{r_{1},r_{2}}(\mu)\right).\mathbb{1}_{\Omega}(\mu).$$

Le premier élément de cette somme correspond au produit dans le domaine spatial d'une fonction qui s'annulle sur l'anneau avec le fond à harmonique. Le deuxième élément est l'anneau bien échantillonné.

De cette manière l'image est bien échantillonnée. Cette construction permet d'avoir un jeu de couples d'orientations sur les contours du cercle. Certains peuvent localement ressembler à de l'aliasing. L'image fournie dans cette base est présentée sur la figure ci dessous :

L'image de gauche est construite selon le modèle ``cercle sur onde''. A droite on a représenté le module de sa transformée de Fourier. Un bon algorithme de détection d'aliasing ne doit pas la détecter aliasée. Sur les contours des deux cercles, on peut observer un grand nombre de couples d'orientations, on peut donc avoir localement une ressemblance avec un effet d'aliasing.

Deux zones spatialement séparées

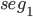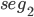Comme nous l'avons vu à plusieurs reprises, le module de la transformée de Fourier seul ne permet pas de détecter l'aliasing. On a présenté dans le chapitre 2 une méthode de construction de segments non aliasés. Considérons deux tels rectangles $seg_{1}$ et $seg_{2}$, on définit alors une image 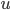$u$ dont la zone correspondant à un seul des deux rectangles est aliasée. La construction se fait par le biais des images suivantes,

$$\hat{\bar{u}}_{1}(\mu)=\delta_{f_{0}}+\delta_{2f_{0}}+\delta_{-f_{0}}+\delta_{-2f_{0}}$$

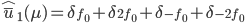
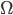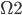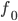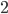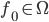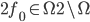Notons $\Omega$ l'espace admissible de Shannon pour un sous-échantillonnage de 2 et $\Omega{2}$ l'espace de Shannon à la résolution considérée. $f_{0}$ sera choisie de manière à ce que pour un sous-échantillonnage de $2$, $f_{0}\in\Omega$ et $2f_{0}\in\Omega{2}\setminus\Omega$. Il correspond alors à 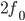$2f_{0}$ une translation élémentaire d'aliasing 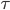$\tau$ telle que 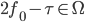$2f_{0}-\tau\in\Omega$. La deuxième image est

$$\hat{\bar{u}}_{2}(\mu)=\delta_{2f_{0}-\tau}+\delta_{-2f_{0}+\tau}$$

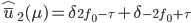
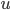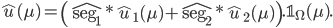
On construit alors l'image $u$,

$$\hat{u}(\mu)=\left(\hat{\text{seg}_{1}}*\hat{u}_{1}(\mu)+\hat{\text{seg}_{2}}*\hat{u}_{2}(\mu)\right).\mathbb{1}_{\Omega}(\mu).$$

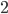L'image utilisée dans le benchmark sera le sous-échantillonnage de rapport 2 de cette image. De l'aliasing est présent sur le segment $1$ alors que le segment $2$ ne présente pas d'aliasing. De plus, la deuxième harmonique du premier segment se replie exactement sur l'harmonique du deuxième segment.

\noindent L'image de ce modèle fournie dans la base est présentée sur la figure ci dessous :

Deux zones spatialement séparées.}{Deux zones spatialement séparées.}{L'image de gauche a été construire grâce au modèle à ``deux zones''. A droite on représente le module de sa transformée de Fourier. Le rectangle de gauche est constitué de deux harmoniques dont la deuxième est aliasée alors que le rectangle de droite est constitué d'une seule harmonique qui correspond exactement à la fréquence de l'harmonique aliasée précédente. Le rectangle de gauche est aliasé, pas celui de droite.

Bruit poivre et sel

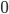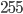le bruit poivre et sel consiste à aléatoirement fixer à $0$ou $255$ le niveau de gris de pixels choisis aléatoirement. Ce bruit peut être appliqué à l'une des images précédentes.

Ce type de pixel isolé ne correspond pas forcément à de l'aliasing, mais peut correspondre à une structure réelle très mal échantillonnée. Il n'est pas évident dans le cas général de décider s'il s'agit d'aliasing ou non.

Dans le benchmark, ce type de bruit a été ajouté à l'image obtenue par phase aléatoire, elle est représentée sur la figure ci-dessous :

L'image de gauche correspond à l'image de la figure \ref{randPhas} à laquelle on a rajouté un bruit poivre et sel. A droite, on a représenté le module de sa transformée de Fourier. 

Images bien échantillonnées

Les 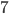$7$ images suivantes ont été choisies en tant que représentantes des cas d'images semblables d'un certain point de vue à de l'aliasing.

Faux aliasing apparent

Une image bien échantillonnée au sens de Shannon est une image dont les seuls échantillons permettent de retrouver exactement les niveaux de gris originaux. Pour autant, à une résolution donnée, une image bien échantillonnée peut laisser apparaitre des effets ressemblants à de l'aliasing qui disparaissent après interpolation. C'est cet effet qui est illustré par l'image représentée à la figure ci-dessous :

L'image de gauche, que l'on appellera ``cartier'' est la photographie d'un bâtiment constitué de barres parallèles. A droite on a représenté sa transformée de Fourier. Du fait de la perspective, ces barres sont de plus en plus resserrées. La procédure utilisée de création de cette image garantit la quasi-absence d'aliasing, par conséquent, tous les effets visibles sont dus à la présence de fréquences très proches de la limite de Shanon dans l'image. 

Angle droit tourné

Les images satellitaires contiennent beaucoup d'angles droits notamment du fait des bâtiments. Lorsque cet angle droit est tourné à 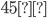$45°$, la figure peut spectralement ressembler à de l'aliasing comme l'illustre la figure ci-dessous :

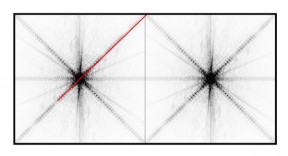
Cette image représente deux modules de transformés de Fourier de l'image ``domo'' de la figure \ref{domo} mis l'un à coté de l'autre (selon la même translation due au sous-échantillonnage). On remarque que dans cette configuration d'angle droit tourné, les plus hautes fréquences de l'une des directions de l'angle droit sont alignées avec la droite correspondant à l'orientation de l'autre direction de l'angle droit. On pourrait ainsi considérer par erreur ce cas comme étant un effet d'aliasing.

Cette image teste la capacité des algorithmes à différencier les angles droits naturels d'un aliasing, elle est présentée sur la figureci-dessous :

L'image de gauche, que l'on appellera ``domo'' est constituée de nombreux angles droits tournés à ``45''. A droite on a représenté sa transformée de Fourier. Ceux-ci peuvent être à tort considéré comme de l'aliasing par un algorithme analysant la géométrie spectrale. 

Faux aliasing spectral

L'image de la figure ci-dessous présente un module de la transformée de Fourier qui parait aliasé du fait de l'alignement d'harmoniques. Or, les différentes harmoniques concernées proviennent de domaines spatiaux différents de l'image, elle n'est pas aliasée.

L'image de gauche, que l'on appellera ``tigre'' a un module de transformée de Fourier (représenté à droite) qui peut sembler aliasé : Les fréquences des rayures du livre au sol correspondent à d'hypothétiques harmoniques aliasées des rayures du livre sur la table. Or, ces différentes harmoniques ne correspondent pas au même livre. Un bon algorithme de détection ne détectera pas d'aliasing dans cette image. La transformée de Fourier de cette image est présentée sur la précédente.

Limite du problème mal posé

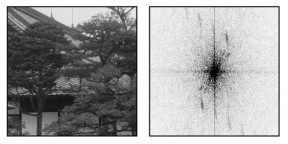
Certaines images réelles peuvent présenter des structures qui localement présentent une relation spectrale d'aliasing. C'est le cas du toit de l'image de la figure ci-dessous. Il s'agit donc dans cette image de tester la capacité à différentier de l'aliasing de cas localement très ressemblant à cet artefact.

\mettreUneFig{temple.jpg}{1}{Limite du problème mal posé.}{Limite du problème mal posé.}{L'image de gauche sera appelée ``temple''. A droite on a représenté le module de sa transformée de Fourier. Le toit de ce temple est constitué de tuiles qui prises sous cet angle forment une structure localement similaire à de l'aliasing. L'image est pourtant bien échantillonnée. }{temple}

Textures

Les images texturées peuvent localement ressembler à des artefacts d'aliasing. Avec l'image de la figure ci-dessous, il s'agit de tester la capacité d'un algorithme à différencier une texture d'un cas d'aliasing.

L'image de gauche que l'on appellera ``arbre'' est un exemple de texture pour laquelle il est très complexe de décider s'il y a aliasing ou non. En l'occurence dans ce cas, l'image est bien échantillonnée. A droite on a représenté sa transformée de Fourier.

Mélange

Les deux dernières images de cette base mélangent les tests précédents. Elles sont bien échantillonnées et présentées ci-dessous :

Les deux dernières images de cette base mélangent les différents tests précédents. En haut, l'image sera appelée ``racines'' et en bas ``vélo''. A droite est représentée la transformée de Fourier de l'image de gauche.

Images mal échantillonnées

Les images aliasées suivantes sont représentatives des cas d'aliasing les plus courants et les plus mal posés. Ces images comportent donc un effet d'aliasing.

Aliasing vertical

Les cas de mauvais échantillonnage d'une structure verticale ou horizontale sont similaires à de l'aliasing 1D. Ce cas est beaucoup plus compliqué qu'un mauvais échantillonnage dans une autre direction, car la direction de l'alias est la même que la partie basse fréquence. L'image ``porte'' présentée sur la figure ci-dessous est un exemple de ce type d'aliasing.

L'image nommée ``porte'' est un exemple d'aliasing vertical. A droite on a représenté le module de sa transformée de Fourier.

aliasing périodique

Lorsque l'on a une répétition périodique, l'aliasing peut être plus étendu spatialement. L'image de la figure ci-dessous présente ce type de structures.

L'image de gauche, appelée ``cartes'', est un exemple d'aliasing périodique. A droite on a représenté le module de sa transformée de Fourier. Les cartes forment des niveaux clairs et foncés se répétant périodiquement. Le sous-échantillonnage brutal crée une oscillation perturbatrice caractéristique.

aliasing directionnel

Les contours contrastés présentent un effet de marche d'escalier qui diffère selon l'orientation. L'image de la figure ci-dessous permet de tester la détection d'aliasing des contours sur un grand nombre de directions.

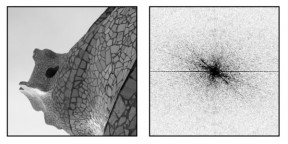
L'image de gauche sera appelée ``gaudi''. A droite on a représenté le module de sa transformée de Fourier. Le carrelage de cette cheminée permet de tester l'aliasing de contours contrastés dans un grand nombre de directions.

Lignes interrompues

Une ligne mal échantillonnée peut apparaitre comme étant une suite de segments interrompus. L'image de la figure ci-dessous présente plusieurs effets de ce type.

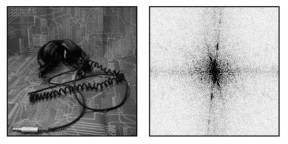Les tracés sur le papier au fond de l'image de gauche forment des lignes interrompues après un sous-échantillonnage brutal. Cette image portera le nom ``music''. A droite on a représenté le module de sa transformée de Fourier.

Mélange

Les trois dernières images présentées sur la figure ci-dessous comportent plusieurs des cas présentés dans les images précédentes.

Ces dernières images regroupent plusieurs des exemples typiques d'aliasing présentés sur les autres images de la base. de gauche à droite, les images en haut seront nommées ``barrault'', ``cachan'' et ``butokai''. En bas on a représenté le module de la transformée de Fourier de l'image du haut correspondante.

La base de test est téléchargeable ici est est accompagnée des originaux pour les images aliasées.